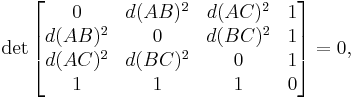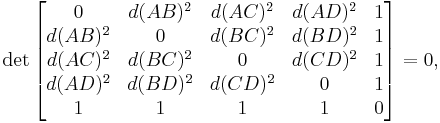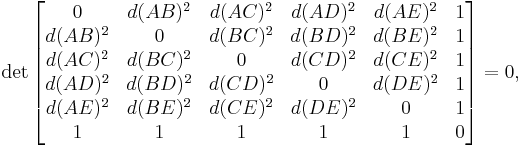Distance geometry

Distance geometry is the characterization and study of sets of points based only on given values of the distances between member pairs. Therefore distance geometry has immediate relevance where distance values are determined or considered, such as in surveying, cartography and physics.

1 Introduction
2 Discussion
3 Cayley–Menger determinants
4 Software for distance geometry
5 References
6 See also

Introduction

The Distance Geometry Problem (DGP) is the problem of finding the coordinates of a set of points starting from the distances between pairs of such points,^[1]^[2]^[3]^[4],.^[5] Such a problem is nowadays much studied by the scientific community, because there are real-life applications that lead to the formulation of a DGP. As an example, an interesting application is the problem of locating sensors in telecommunication networks. In such a case, the positions of some sensors are known (which are called anchors) and some of the distances between sensors (which can be anchors or not) are known: the problem is to locate the positions of all the sensors.

Many other real-life applications that can be formulated as DGPs arise in biology and chemistry. For example, some models for protein predictions are based on a DGP, and also some models for protein docking. However, in this field, the most studied problem is the following. The coordinates of the atoms of a given molecular conformation are to be discovered by exploiting only some of the distances between pairs of atoms found by experimental techniques. If this is the case, the problem is known in the literature as the Molecular Distance Geometry Problem (MDGP).

Discussion

A straight line is the shortest path between two points. Therefore the distance from A to B is no bigger than the length of the straight-line path from A to C plus the length of the straight-line path from C to B. This fact is called the triangle inequality. If that sum happens to be equal to the distance from A to B, then the three points A, B, and C lie on a straight line, with C between A and B.

Similarly, suppose one knows

the distance from A to B;
the distance from A to C;
the distance from A to D;
the distance from B to C;
the distance from B to D; and
the distance from C to D.

Knowing only these six numbers, one would like to figure out

whether A, B, C, and D lie on a common straight line;
whether A, B, and C lie on a common line but D is not on that line (and similarly for any of A, B, and C in the role of the one exceptional point);
whether all four points lie in a common plane;
if they lie in a common plane, whether one of them is in the interior of the triangle formed by the other three, and if so, which one.

Distance geometry includes the solution of such problems.

Cayley–Menger determinants

Of particular utility and importance are classifications by means of Cayley–Menger determinants, named after Arthur Cayley and Karl Menger:

a set Λ (with at least three distinct elements) is called straight iff, for any three elements A, B, and C of Λ,

$\det \begin{bmatrix} 0 & d(AB)^2 & d(AC)^2 & 1 \\ d(AB)^2 & 0 & d(BC)^2 & 1 \\ d(AC)^2 & d(BC)^2 & 0 & 1 \\ 1 & 1 & 1 & 0 \end{bmatrix} = 0,$

a set Π (with at least four distinct elements) is called plane iff, for any four elements A, B, C and D of Π,

$\det \begin{bmatrix} 0 & d(AB)^2 & d(AC)^2 & d(AD)^2 & 1 \\ d(AB)^2 & 0 & d(BC)^2 & d(BD)^2 & 1 \\ d(AC)^2 & d(BC)^2 & 0 & d(CD)^2 & 1 \\ d(AD)^2 & d(BD)^2 & d(CD)^2 & 0 & 1 \\ 1 & 1 & 1 & 1 & 0 \end{bmatrix} = 0,$

but not all triples of elements of Π are straight to each other;

a set Φ (with at least five distinct elements) is called flat iff, for any five elements A, B, C, D and E of Φ,

$\det \begin{bmatrix} 0 & d(AB)^2 & d(AC)^2 & d(AD)^2 & d(AE)^2 & 1 \\ d(AB)^2 & 0 & d(BC)^2 & d(BD)^2 & d(BE)^2 & 1 \\ d(AC)^2 & d(BC)^2 & 0 & d(CD)^2 & d(CE)^2 & 1 \\ d(AD)^2 & d(BD)^2 & d(CD)^2 & 0 & d(DE)^2 & 1 \\ d(AE)^2 & d(BE)^2 & d(CE)^2 & d(DE)^2 & 0 & 1 \\ 1 & 1 & 1 & 1 & 1 & 0 \end{bmatrix} = 0,$

but not all quadruples of elements of Φ are plane to each other;

and so on.

Software for distance geometry

DGSOL. It is based on the idea of approximating the penalty function with a sequence of smoother functions converging to the original objective function. It is usually used for performing comparisons to other newly proposed techniques, whose code is often not released. DGSOL solves distance geometry problems where a lower and an upper bound on the distances are available.
MD-jeep. This software is based on a combinatorial reformulation of the distance geometry problem. A Branch & Prune algorithm is implemented for an efficient solution of the reformulated problem. It has been mainly applied to distance geometry problems related to protein molecules.
Xplor-NIH. It has been particularly designed for solving instances of the problem in which the data come from NMR experiments, and it includes different functionalities. In particular, for the solution of the distance geometry problems, it makes use of heuristic methods (such as Simulated Annealing) and local search methods (such as Conjugate Gradient Minimization).
TINKER. This is a package for molecular modeling and design. It includes many force fields for attempting the prediction of protein conformations from their chemical structure only. One of its functionalities, however, is to solve distance geometry problems.

References

^ Blumenthal, L.M. (1970). Theory and applications of distance geometry (2nd ed.). Bronx, New York: Chelsea Publishing Company. pp. 347. ISBN 0-8284-0242-6. LCCN 79113117.
^ Crippen, G.M.; Havel, T.F. (1988). "Distance Geometry and Molecular Conformation". John Wiley & Sons.
^ Liberti, L.; Lavor, C.; Maculan, N. (2008). "A Branch-and-Prune Algorithm for the Molecular Distance Geometry Problem". International Transactions in Operational Research 15: 1–17.
^ Mucherino, A.; Liberti, L.; Lavor, C.; Maculan, N. (2009). "Comparisons between an Exact and a MetaHeuristic Algorithm for the Molecular Distance Geometry Problem". ACM Conference Proceedings, Genetic and Evolutionary Computation Conference (GECCO09): 333–340.
^ More, J.J.; Wu, Z. (1999). "Distance Geometry Optimization for Protein Structures". Journal of Global Optimization 15: 219–223.